Volume and surface area computation for triangle meshes.

Warning! This method works only for watertight meshes.

Volume computation

Using the notations defined in the following figure: 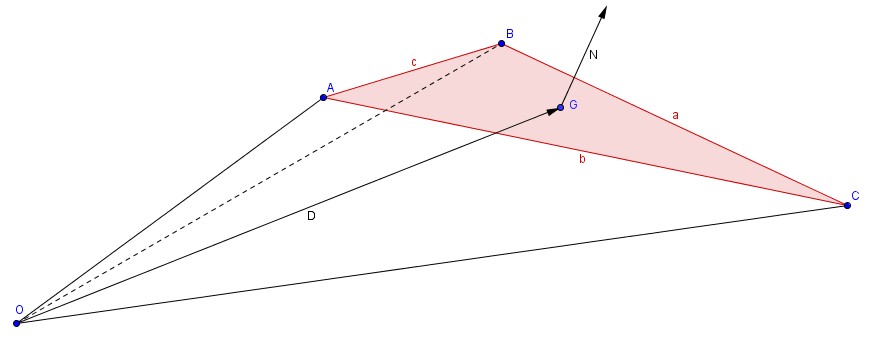volume of a tetrahedron Figure 1: volume of a tetrahedron

The surface area of the face $ABC$ can be computed as \begin{equation} Area(ABC) = \frac{ \vert \vec{AB} \times \vec{AC} \vert } {2} \end{equation}

Let us now consider the volume of a tetrahedron by adding a point $O$ (e.g., ). The volume of $OABC$ is then defined as: \begin{equation} Volume(OABC) = \frac{1}{3} . \frac{ \vert \vec{AB} \times \vec{AC} \vert } {2}. \vert \vec{OG}.\vec{N} \vert, \end{equation} with $\vert \vec{OG}.\vec{N} \vert$ the height of the tetrahedron.

The final volume is obtained by integrating the volume of the tetrahedron defined for each face. However, not all tetrahedron should be added. This idea is illustrated for a 2D case in the following figure: one-ring neighbourhood

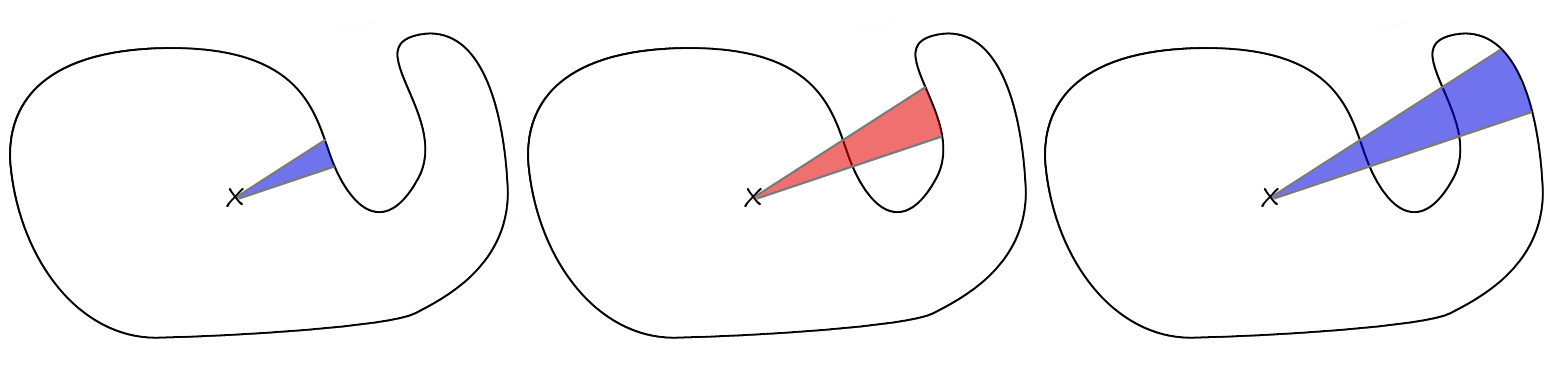
The areas in blue should be added, and the areas in red should be removed during the integration. This is performed by considering the sign of the dot product between $\vec{OG}$ and the normal of the face $\vec{N}$ (in practice, we simply remove the norm used above). The final formula of the volume integration is: \begin{equation} Volume = \sum_{f \in F} \frac{1}{3} . \frac{ \vert \vec{AB} \times \vec{AC} \vert } {2}. (\vec{OG} . \vec{N}) \end{equation}

Similarly, the surface area of the mesh can be obtained with: \begin{equation} Area = \sum_{f \in F} \frac{ \vert \vec{AB} \times \vec{AC} \vert } {2} \end{equation}

Info! Any points O can be used for the computation of the volume.

Validation

Example of volume computed on the following dataset

volume validation cube volume validation cylinder

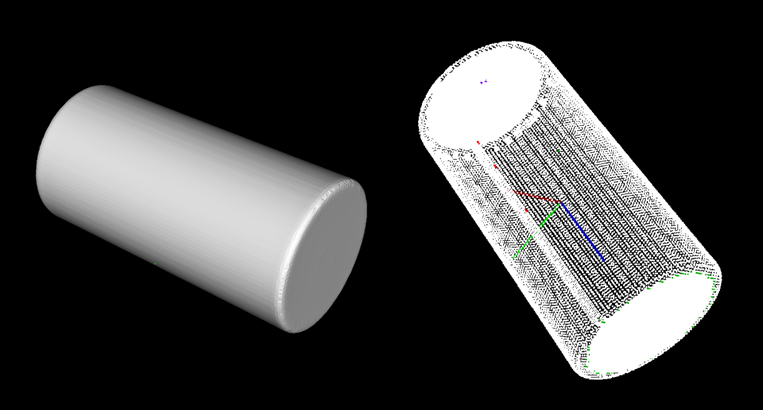
Tables computed value real value relative error
volume cube $64.174 m^3$ $64.0 m^3$ $0.0027$
surface area cube $90.652 m^2$ $96.0 m^2$ $0.0557$
volume cylinder $12.536 m^3$ $12.566 m^3$ $0.0024$
surface area cylinder $30.981 m^2$ $31.416 m^2$ $0.0138$
Info! The error actually comes from the Poisson surface reconstruction.

Data

The data and the code is available here (in C++ with PCL as a dependency), we start from a point cloud with the surface reconstructed using Poisson surface reconstruction1.

one-ring neighbourhood one-ring neighbourhood one-ring neighbourhood
cube.ply cylinder.ply volume_code.zip

References

  1. M. Kazhdan, M. Bolitho, and H. Hoppe, Poisson surface reconstruction, In SGP ’06: Proceedings of the fourth Eurographics symposium on Geometry processing. ↩