Discrete Differential Geometry

Serie of notes on discrete differential-geometry.

Info! Unfinished notes

Content

• discrete differential operators
• definition of the operator with the vertex as a reference
• implementation with respect to the one-ring neighbourhood

List of ressources:

• Stanford slides
• Hao Li slides
• AIM@shape
• Markdown cheat sheet

Discrete differential-geometry operators

Gradient

\begin{equation} \nabla f = \big( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \big) \notag \end{equation}

$$\nabla f(x) = (f_j - f_i) \frac{(x_i-x_k)^\bot}{2A_T} + (f_k - f_i) \frac{(x_j-x_i)^{\bot}} {2A_T}$$

Divergent

$$\nabla . f = \frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}$$

Curl

Laplace-Beltrami operator

The Laplace operator is defined in the Euclidean space as: \begin{equation} \Delta f = \nabla \cdot \nabla .f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}. \end{equation}

The Laplace-Beltrami operator, noted $\Delta_s$, generalizes the Laplacian to surfaces (i.e., 2D manifolds) and is defined with respect to the curvature.

Relation with curvature: Let’s first define the curvatures on continuous surfaces before to formulate it into discrete surfaces, following the notations from Meyer et al.¹.

Given a surface $S$, a point $p$, its associated normal vector $\mathbf{n}$, and a unit vector $\mathbf{e}_\theta$; the notion of normal curvature $\kappa^N(\theta)$ is locally defined as the quantification of the curvature in the plane $\{p, \mathbf{n}, \mathbf{e}_\theta \}$. The two principal curvatures $\kappa_1$ and $\kappa_2$ and the associated orthogonal directions $\mathbf{e}_1$ and $\mathbf{e}_2$ are the extremum values of the normal curvature. The mean curvature $\kappa_H$ is defined as \begin{equation} \kappa_H = \frac{1}{2\pi}\int^{2\pi}_0\kappa^N(\theta)d\theta, \end{equation} which can be simplified using the principal curvatures as $\kappa_H = \dfrac{\kappa_1 + \kappa_2}{2}$. Additionally, the Gaussian curvature $\kappa_G$ is defined as $\kappa_G = \kappa_1\kappa_2$.

The Laplace-Beltrami operator $\mathbf{L}(p)$ is defined as $\mathbf{L}(p) = 2\kappa_H(p)\mathbf{n}(p)$. The integration of the Laplace-Beltrami operator is then defined as

\begin{equation} \int\int_{A}\mathbf{L}(\mathbf{x})d(A) = \frac{1}{2}\sum_{j\in N(i)}(\cot{\alpha_{ij}} + \cot{\beta_{ij}})(\mathbf{x}_i - \mathbf{x}_j). \label{eq:Laplacian_integration} \end{equation}

Let us now consider a vertex and it’s own one ring neighbourhood defined as follow:

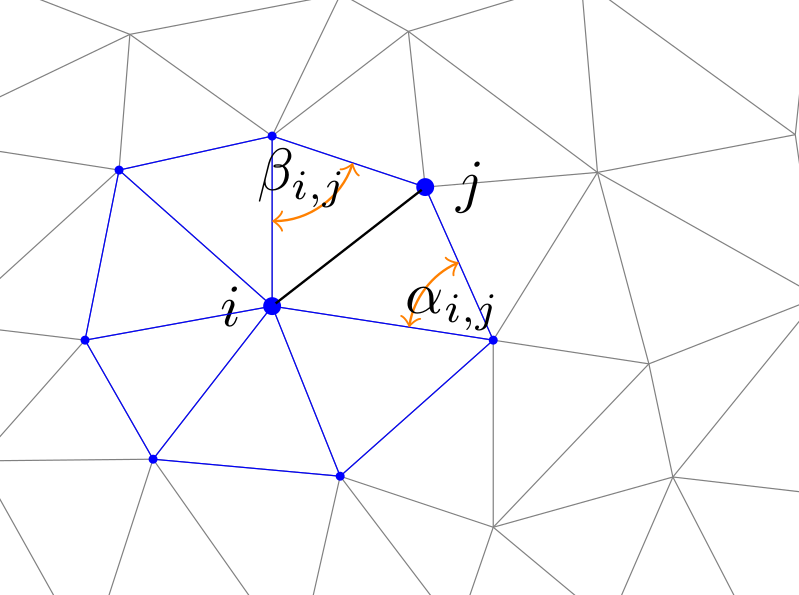
A more practical Laplace-Beltrami Operator implementation is to store the right hand side of equation \eqref{eq:Laplacian_integration} under a $n \times n$ sparse matrix form $\mathbf{L}$ where each elements is the vertex to vertex relationship such as:

$$\boldsymbol{L}_{ij} = \begin{cases} \frac{1}{2}\sum_{i\neq j} \cot \alpha_{ij} + \cot \beta_{ij} & \text{if } i = j,\\ -\frac{1}{2} \cot \alpha_{ij} + \cot \beta_{ij} & j \in \mathcal{N}(i),\\ 0 & j \notin \mathcal{N}(i). \end{cases}$$

With a one ring neighbourhood defined as follow:

The C++ pseudo-code of that cotangent Laplacian (for a sparse matrix):

for(int i : vertices)
{
  for(int j : one_ring(i))
  {
    for(int k : triangle_on_edge(i,j))
    {
      L(i,j) = cot(angle(i,j,k));
      L(i,i) -= cot(angle(i,j,k));
    }
  }
}

In practice more efficient implementation can be used, see libigl implementation for more details.

Mass matrix

Warning! This formula is easy to compute but is slightly wrong for obtuse triangles (angles $> 90^\circ$).

The mass matrix defined here is the area of the polygon where each point is the barycenter of each triangle (barycentric cells). The are computed is the part filled in blue in the following figure:

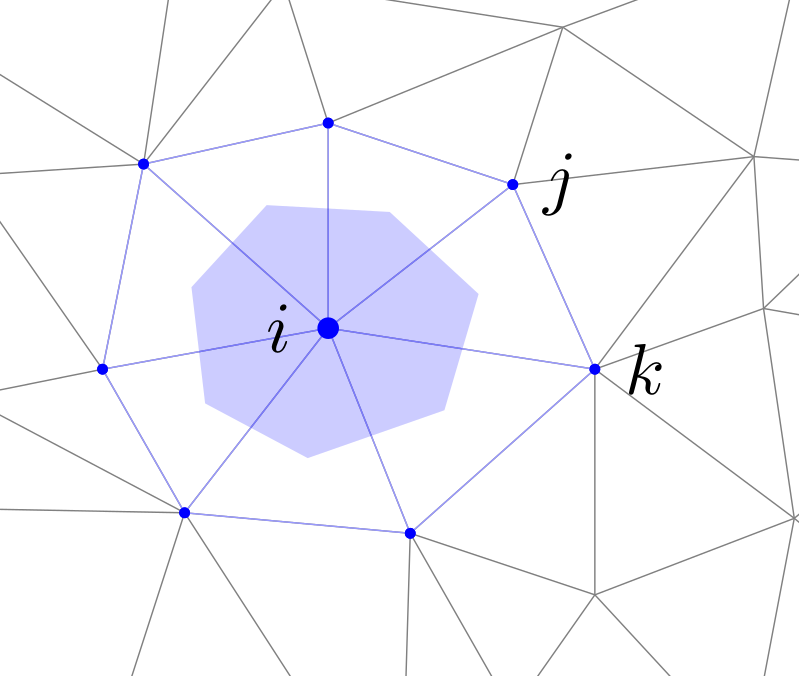
With A, an $n$ by $n$ diagonal matrix:

for(int i : vertices)
{
  for(int j : one_ring(i))
  {
    for(int k : triangle_on_edge(i,j))
    {
      area = (j-i).cross(k-i).norm() / 2;   // get area of the face
      local_area = area / 3;                // get the are towards the barycenter
      A(i, i) += local_area / 2;                  // / 2 because added twice
    }
  }
}

References

1. M. Meyer, M. Desbrun, P. Schroder, and A. H. Barr, Discrete Differential-Geometry Operators for Triangulated 2-Manifolds, Springer, 2003. ↩